「大学への数学 1対1対応の演習」は、受験生に愛用され続けている受験数学の王道参考書・問題集です。
今回は大学への数学1対1対応の演習のすべてを解説します。
- 1対1対応の演習はいつから使うべき？
- 1対1対応の演習のレベルは？
- 1対1対応の演習の効果的な使い方は？
- 1対1対応の演習の問題数は？
これを読めば「1対1対応の演習」についてバッチリわかります！
✔︎記事の信頼性
▼筆者の受験結果はこちら▼
▼筆者の模試結果はこちら▼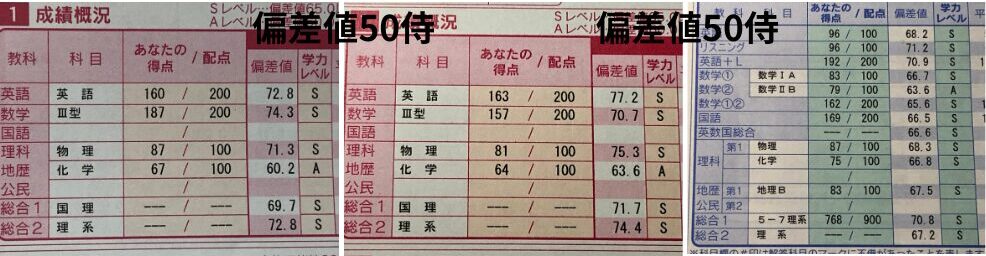
大学への数学1対1対応の演習のいつから使うべき？
「大学への数学1対1対応の演習」は「教科書レベルの知識がついてから」使うべきです。
時期としては、高2のうちに数学ⅠA～ⅡB編に手を付けるのがおすすめ。
遅くても高3の夏には使いはじめたい問題集です。
大学への数学1対1対応の演習のレベル
「大学への数学1対1対応の演習」のレベルは「共通テスト～理系国公立標準」です。
文系・理系問わず、多くの人が受験終盤まで使えます。
「1対1対応の演習」に載っている問題が完璧に解けるようになれば、ほとんどの大学で合格点が取れるレベルに到達します。
大学への数学1対1対応の演習の問題数とページ数
「大学への数学1対1対応の演習」の問題数は以下の通りです。
| 冊子 | ページ数 | 問題数 |
| 大学への数学1対1対応の演習 数学Ⅰ | 116p | 103 |
| 大学への数学1対1対応の演習 数学A | 120p | 108 |
| 大学への数学1対1対応の演習 数学Ⅱ | 164p | 166 |
| 大学への数学1対1対応の演習 数学B | 112p | 118 |
| 大学への数学1対1対応の演習 数学Ⅲ 曲線・複素数編 | 104p | 150 |
| 大学への数学1対1対応の演習 数学Ⅲ 微積分編 | 152p | 86 |
大学への数学1対1対応の演習の効果的な使い方
「大学への数学1対1対応の演習」を愛用していた私が、効果的な使い方を偏差値別に紹介します。
偏差値60未満の人はこう使おう
偏差値60未満の人は、まず解法を知ることが重要です。
解法を知るためには、次のように「1対1対応の演習」を使うと効果的です。
- ヒントを参考にしながら例題を解く
- 模範解答と見比べて修正する
- 次の例題へ（演習問題は飛ばしてOK！）
このサイクルを繰り返しましょう。
まず、ヒントを参考にしながら例題を自分なりに解いてみることから始めてください。
- 解き終わった
- これ以上分からない
という状態になったら、自分の解答と模範解答を比べましょう。
模範解答を見ながら、自分の解答を修正します。
このとき、単なる丸写しではなく、模範解答を自分なりに解釈するのがコツです。
自分の言葉で説明できるように、解説を上から1つ1つ噛み砕いて理解しましょう。
もし途中で分からない文言が出てきたら、「要点の整理」に戻って調べることも大切です。
各ページの下方に掲載されている演習問題はかなり難しいです。
発想力も必要になってくるので飛ばしてOKです。
例題を解くだけなので、時間はそれほどかからず終わるはず。
2周くらいすれば、基礎的な解法は身についているでしょう。
偏差値60～65の人はこう使おう
偏差値60～65に到達した人は解法がある程度身についています。
ここから偏差値を上げるためには、思考力や発想力を鍛えていくことが必要です。
思考力と発想力を鍛える方法は、「演習問題を解く」です。
演習問題はかなり難しいです。
例題の模範解答に載っている解き方だけでは解けないことも多いでしょう。
この「＋α」こそが思考力や発想力です。
違う角度から問題を捉えてみたり、他の例題で使った解法を組み合わせてみたり。
このように問題に対してじっくり向き合う過程で、思考力や発想力が身についていきます。
偏差値65以上の人はこう使おう
偏差値65以上の人は「大学への数学1対1対応の演習」をサブの問題集として使いましょう。
メインに使うべきは、別の問題集です。
・やさしい理系数学
・大学の過去問
などなど
基本的に、これらの問題集で演習しましょう。
問題を解いている途中で不明な点があったら、「1対1対応の演習」に戻って解法や考え方を再度確認します。
「1対1対応の演習」は分野ごとに整理されているので、該当部分を探すのに時間はかかりません。
何度も何度も再確認を繰り返すうちに、徐々に「1対1対応の演習」に戻る必要がなくなってきます。
最終的には「1対1対応の演習」（＝受験数学の辞書）が一切必要なくなるほど、解法や考え方を理解して応用できるようになるのが理想です。
大学への数学1対1対応の演習の良い評判・口コミ
「大学への数学1対1対応の演習」の良い評判・口コミを調査してまとめました！
（今回の参照元：amazon）
典型問題を効率よく学べる
「1対1対応の演習」に載っているのは典型問題が多いです。
入試数学に必要な基本的な解法・考え方を効率よく学べます。
問題数が少ないので短期間で成績が上がる
ほかの問題集と比べて、問題数が少ないのも「1対1対応の演習」の特徴。
例えば数学ⅠA合わせて、例題が107問しかありません。
青チャートのⅠAだったら300問以上の例題があります。
そのため、短期間で数学の成績を上げたい人に向いています。
大学への数学1対1対応の演習の悪い評判・口コミ
「大学への数学1対1対応の演習」の悪い評判・口コミについてもまとめました！
演習問題の難易度がやや高い
特に演習問題の難易度が高いという評判が多かったです。
横に載っているヒントを使っても難しい問題がちらほらあります。
初学者には難しい
あと、最低限教科書レベルの知識がないと使えないという意見もありました。
数学の初学者は使うべきではないかもしれません。
個人的なレビュー（余談）
ここからは余談です。
「大学への数学1対1対応の演習」は6冊子に分かれています。
- 「数学Ⅰ」編
- 「数学A」編
- 「数学Ⅱ」編
- 「数学B」編
- 「数学Ⅲ微積分」編
- 「数学Ⅲ曲線・複素数」編
その理由は以下の通り。
- そもそも数学Bのベクトルと数列が試験に出てきやすい
- 解説が簡潔に整理されており単純明快で分かりやすい
- 本が薄いのですぐに終わらせやすい
- ⅠAとⅡB融合問題も取り扱っている
ベクトルや数列の問題は作りやすいうえ、大学でも必須級の知識なので、試験に出る回数が非常に多いです。
そのため、ベクトルと数列ができるようになれば、試験の点数が一気に伸びます。
「1対1対応の演習 数学B編」は良問揃い。そのうえ、解説が短くて分かりやすいです。
また、「1対1対応の演習 数学B編」の後半にはⅠAとⅡBの融合問題もあります。
偏差値60以上の人だったら、思考力を鍛えるために融合問題は最適です。
以上のように、大学受験対策の観点から数学Ｂ編は特に優れています。
ベクトルや数列が苦手な人はもちろん、手っ取り早く点数を上げたい人は、
とりあえず「大学への数学1対1対応の演習 数学Ｂ」を手に取ってみるのがおすすめです。
数学を得点源にしたいなら個別指導を利用しよう
- 数学が苦手
- 数学の点数が伸び悩んでいる
- 問題が解けるようになる気がしない
- 数学を得点源にしたい
という人は、個別指導のトウコベ
を利用するのがおすすめです。
トウコベがおすすめな理由は6つあります。
- 東大生がマンツーマンでわかるまで教えてくれる
- 24時間いつでも質問できる
- オンラインで受けられるから便利
- 授業日以外の家庭学習まで管理してくれる
- 一人ひとりに合わせた勉強計画を作成してくれる
- 授業料は受けた分だけだから料金がリーズナブル
トウコベが気になる人は、無料相談をしてみてください！
＼ 無料で相談できます！ ／
トウコベで相談してみる！
まとめ
「大学への数学1対1対応の演習」のすべてを解説しました。
