今回は高校数学の独学勉強法を解説します。
- 高校数学の勉強法は?
- 独学するのにおすすめの参考書はどれ?
- 数学が苦手な場合はどうすればよい?
この記事を読めば、独学での高校数学の勉強法がばっちり分かります!
✔︎記事の信頼性

▼筆者の受験結果はこちら▼
▼筆者の模試結果はこちら▼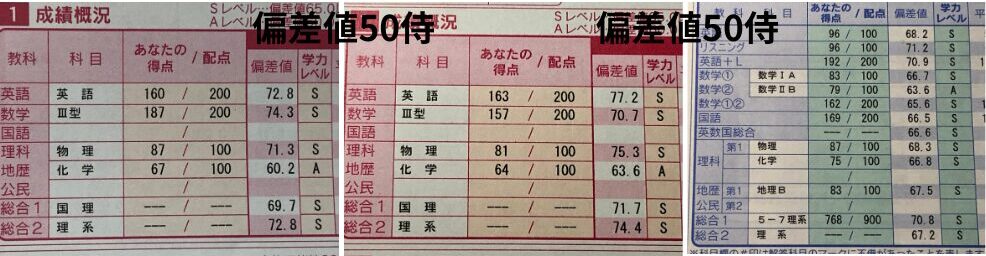
高校数学の独学はきつい?
高校数学は独学でも勉強できる科目です。
しかし、今高校数学が苦手だと感じているなら話は別です。
わからないことが多すぎて挫折する可能性があるので、はっきり言って独学で勉強するのはおすすめしません。
そもそも、高校数学は入試における配点が高いです。
共通テストでは合計200点も配点されていますし、特に理系の場合は国公立2次試験や私立入試で数学力が試されます。
よって、数学ができなければ受験で大きく不利になります。
以上より、高校数学に対して苦手意識があるなら、無理に独学せずに家庭教師を利用してください。
おすすめの家庭教師は「オンライン家庭教師マナリンク」です。
オンライン家庭教師マナリンクがおすすめな理由は5つあります。
- 先生の数が多く、雰囲気・指導方針・カリキュラム・評判を確認して自分の好きな先生を探せる
- 納得できるまで無料体験授業を受けられるので相性の良い先生が見つかる
- 専用アプリで指導日以外にも先生とやりとりできる
- オンラインでいつでもどこからでも質の高い授業を1対1で受けられる
- 料金体系がシンプルで分かりやすい
「数学が苦手」「数学を短期間でできるようになりたい」という方は、ぜひオンライン家庭教師マナリンクを活用してください!
\ 最短その日に無料体験できます! /
マナリンクで無料体験授業を受けてみる!
高校数学に必要な能力
さて、高校数学に必要な能力は以下の3つです。
- 問題を正しく捉える読解力
- 解法を正しく応用する思考力
- 問題を異なる視点から捉える発想力
まず必要なのは読解力です。
問題を正しく捉えられなければ、正しい答えは導き出せません。
続いて必要なのは思考力です。
解法を正しく理解したうえで、問題ごとに適した解法を引き出して応用できるようになれば、たいていの問題は解けるようになります。
さらに、難しい問題を解くために必要になってくるのが発想力です。
発想力があれば発展問題を解けるようになるため、数学の得点でライバルと大きな差を付けられます。
高校数学の独学勉強法
ここからは、高校数学の勉強法を解説します。
問題の読解力を身につける
高校数学を独学で勉強する場合、まずは読解力を鍛えることからはじめます。
読解力があれば、問題を正しく読めるようになります。
逆に、読解力がなければ全くと言っていいほど数学の問題に太刀打ちできません。
問題の読解力を身につけるには、数学の基礎をしっかり勉強することが大切です。
※ここで挙げたのはほんの1例です。ほかにも学ぶべき知識はたくさんあります。
数学の基礎を勉強するときは、体系的に勉強することが大切です。
その理由は、各単元の内容が相互につながっているからです。
解法を応用する思考力を身につける
続いて身につけるべき能力は、解法を応用する思考力です。
思考力が身につけば問題を解くのに最適な解法を選べるようになるため、数学の成績はぐんと伸びます。
逆に、思考力がなければ問題を正しく解けません。
解法を応用するためには、まず解法をしっかり理解することが大切です。
解法を理解するためには、参考書で解法を確認しながら、簡単な問題集で演習しましょう。
・黄チャート
・シグマ基本問題集
・入門問題精講
などなど
ここで使う問題集は何でも大丈夫。教科書や学校で配られた問題集を使ってもOKですよ。
解法をある程度理解したら、解法を応用する練習をはじめます。具体的には、標準レベルの問題集で問題演習しましょう。
・青チャート
・基礎問題精講
などなど
ここも、どの問題集を使っても大丈夫です。
解法を応用する思考力を効率的に身につけるコツは、各問題の解き方をしっかり考えることです。
すぐに解答解説を見るのはNG!どんな問題でも諦めず、分からなくても最低10分は解法を考えましょう。
ここまで紹介した勉強法で、読解力と思考力はばっちり身につきます。
この段階で、ほとんどの大学入試でも合格点を取れるでしょう。
異なる視点から問題を捉える発想力を身につける
ただ、難問を解ききるには発想力が必要です。
ここでいう発想力とは、異なる視点から問題を捉える力を指します。
発想力を鍛えるには、さまざまな難問を初見で解くことが重要です。
知っている限りの解法を使って、試行錯誤しながら問題に向き合ってください。
このとき使うのは、発展レベルの問題集です。
・標準問題精講
・やさしい理系数学
・文系数学の良問プラチカ
などなど
「もう絶対に分からない!」と感じるまで問題と向き合ったら、解答解説を読みます。
このとき、解答解説は自分の言葉で説明できるくらいしっかり読み込むことが大切です。
また、難問に慣れてきたら、「どのアプローチが一番速く解けるのか」という解答スピードを重視してみてください。
解答スピードが速くなれば試験時間に余裕ができ、見直しに使える時間が増えるため、数学で安定して高得点を取れるようになります。
高校数学の独学で使うべきおすすめの参考書・問題集8選
ここからはおすすめ参考書・問題集を紹介します。
やさしい高校数学
高校数学をやさしくかみ砕いて解説する参考書です。
中学の復習を収録する、イラストと図解が豊富に使用するなど、高校数学をなるべく簡単に理解できるように工夫されています。
先生と生徒の会話形式で進んでいくので、スラスラと読み進められるのがポイント。
また、定期テストや共通テストで出題されやすい問題が掲載されているのも魅力です。
やさしい高校数学は、高校数学の初学者におすすめの参考書です。
白チャート
教科書でも難しいと感じた人におすすめの参考書・問題集です。
高校数学の基礎の基礎を徹底して学習できます。
黄チャート
黄チャートは上述の白チャートよりもやや難易度が上がり、教科書レベルから入試基礎レベルまでの必須問題を網羅しています。
基本例題・重要例題・補充例題の3種類に分けられているため、学習状況に合わせて適切に問題演習を積めます。
問題を解くのに必要な定理や公式、定義などの基本事項がまとまったページがあるのがポイント。
演習していて「あれ、どんな公式だっけ」とど忘れしたときにすぐに探せるので便利です。
また、解説がしっかりしていて分かりやすいため、数学の基礎を学習するにはもってこいです。
青チャート
青チャートは非常に人気の参考書・問題集です。
上述の黄チャートよりも難易度は上がり、入試頻出の標準レベルの問題がたくさん載っています。
問題を解くのに必要なポイントや解法・方針の立て方を詳しく説明しているのが特徴。
また、学習効果が高くなるように同タイプの問題が配列されているので、効率的に学習できます。
さらに、基本定着・精選速習・実力錬成という3つのコースがあるので、目的に合わせて問題を絞って演習を積めるのもポイント。
そのうえ、スマホで視聴できる各例題の解説動画が提供されているため、疑問点を解消しやすいのも魅力です。
大学への数学1対1対応の演習
大学への数学1対1対応シリーズは、青チャートと並んで有名な参考書・問題集です。
例題→関連演習題の流れで、各単元のテーマを深く理解できるように設計されています。
「要点の整理」というページでは、単元の問題を解くのに必要な定義、用語、定理、必須事項などがまとまっているのがポイント。
問題を解くときに役立つのはもちろん、教科書にない事柄が載っているため、教科書と入試のレベルの差をしっかり埋められます。
大学への数学スタンダード演習
新数学スタンダード演習は、入試に直結する問題を多数掲載している参考書です。
前述の1対1対応の演習よりやや難易度が高くなっており、着実にレベルアップできます。
分野別の問題のほか、分野横断的な「総合問題」が載っているのが特徴。
さまざまな知識を組み合わせたり、異なる視点から問題を捉えたりする力が身につきます。
また、「ミニ講座」というページでは、より発展的な内容を扱っているのもポイント。
典型ではないけど重要な事項を学習できるので、難関大入試で問われやすい変則問題を解くときに役立ちます。
新数学スタンダード演習は、高校数学の仕上げをしたい人におすすめの参考書です。
やさしい理系数学
やさしい理系数学は、一般性があってさまざまな問題に応用できる問題解法のアプローチに重点を置いた参考書です。
「やさしい」という名とは裏腹に問題の難易度は高く、発想力と数学的センスを磨くのに役立つ中堅~やや難関大学の頻出問題が掲載されています。
解答が充実しているのがポイント。
1つの問題に対して別解が3つ載っていることもあります。
やさしい理系数学は、過去問演習前に数学力を仕上げたい人におすすめの参考書です。
大学の過去問
大学の過去問は実践的に演習するなら最適な問題ばかりです。
しかも、量や種類が豊富なので、たくさん演習できるのも重要なポイントです。
そもそも、市販の問題集に載っている問題ほとんどは、もとをたどれば大学の過去問です。
数学の勉強がある程度に詰まってきたら、過去問を解きまくりましょう。
余裕がある文系は数学Ⅲを勉強するのがおすすめ
数学IIIでは、数学ⅠAやⅡBで学んだことをもう少し深堀りしたり、2次曲線や複素数平面を新たに学習したりします。
「難しそう」と思うかもしれませんが、数学ⅠAやⅡBの基礎力がついていれば大丈夫。
上で紹介した高校数学の勉強法に従って勉強すれば、難なく習得できます。
基本的に、数学IIIは理系の難関大受験者が学ぶ範囲です。
ただ、文系や難関大を受験しない理系でも数学Ⅲを勉強することで、ライバルと大きく差をつけられます。
その理由は、数学Ⅲを学習することで解法の幅がぐんと広がるからです。
解法の幅が広がれば問題を更に素早く解けるようになるため、ライバルと圧倒的な差をつけられます。
上述のように、数学Ⅲの学習難易度は、思っているよりも高くありません。
余裕のある方は、数学Ⅲを学ぶのがおすすめです。
数学が得意でも共通テスト数学が苦手な人は多い
ここからは共通テストについて簡単にお話します。
共通テスト数学は200点という高配点の重要科目です。そのため、安定して高得点を取れれば、大きなアドバンテージになります。
しかし、「数学が得意だけど共通テスト数学は苦手」という人は多いです。その原因として、たとえば以下が考えられます。
- マーク形式に慣れていない
- 計算スピードが遅く精度が悪い
- 情報の取捨選択ができていない
ライバルに差をつけられないため、そしてライバルと差をつけるためには、それぞれの原因に対して適切に対処することが大切です。
- 普段からマークする習慣をつける
- 計算のコツを身につける
- 無駄な情報の読解に時間を使わない
まとめ
数学の独学勉強法を解説しました。
最近は塾や予備校に通わず、独学で大学受験する人が増えています。その理由は、インターネットの発達や参考書など教材の充実により、個人でも勉強できる環境が整っているからです。 とはいえ、こんなふうに考えている人も[…]
中学生の時は数学が得意だったのに、高校数学になると全くわからず成績が落ちた もともと数学は苦手だったけど、高校に入ってさらにわからなくなったという悩みを持っている学生は多いですよね。筆者実際、私も中[…]















